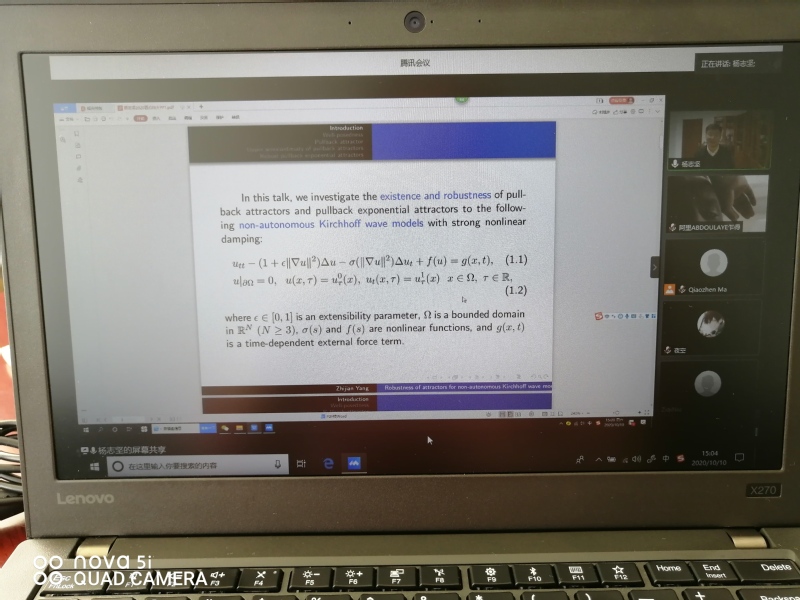
10月10日,应学院邀请,郑州大学二级教授、博士生导师杨志坚在线为bat365官网师生作了题为《Robustness of attractors for non-autonomous Kirchhoff wave models with strong nonlinear damping》的学术报告。报告会由学院马巧珍教授主持,相关专业师生60余人在线观看了报告。
杨志坚教授对具有强非线性阻尼的非自治基尔霍夫波模型在非线性项的增长指数达到超临界范围时,方程解的适定性、拉回吸引子的存在性及上半连续性和拉回指数吸引子的鲁棒性等方面做了详细讲解。整个报告时长2小时,包括主题讲解和在线问答,杨志坚教授首先介绍了研究该模型的初衷和背景,然后详细讲解了当非线性项的增长指数达到超临界范围时,为了处理和克服研究过程中遇到的困难和问题,提出了一种新的方法来研究超临界非线性条件下拉回吸引子的上半连续性和拉回指数吸引子的稳定性。最后杨志坚教授对这类问题的后续研究和发展做了深刻的剖析及讲解,同时回答了在线师生提出的相关问题。
【报告人简介】
杨志坚,郑州大学理学博士、日本九州大学数理学博士、郑州大学二级教授、博士生导师,河南省跨世纪学术技术带头人,河南省数学会常务理事。现任美国《Mathematical Reviews》评论员,《Journal of Partial Differential Equations》编委。先后多次主持国家自然科学基金,河南省自然科学基金项目。主要研究来自物理、力学和量子力学中的非线性发展方程及对应的无穷维动力系统的长时间行为。在具有不同类型阻尼的Kirchoff型方程、具p-拉普拉斯型非线性应变的波动方程、Boussinesq型方程、非线性梁方程等的适定性、正则性和吸引子问题等方面都做出了研究成果,在《J.Differential Equations》《Nonliearity》《Commun. Contemp. Math》《Applied Mathematics and Optimization》《Discrete Contin. Dyn. Syst.》《Appl. Math Lett.》等SCI期刊发表论文70多篇。